Demystifying monads in Rust through property-based testing
Table of contents
In programming pedagogy, monads have a place as a mystical object from the functional programming world that’s hard to understand and even harder to explain. The stereotype about monad explanations is that they fall into two buckets: either comparisons to some kind of food item, or throwing complex mathematical jargon at you, what’s the problem?
But monads aren’t esoteric or magical at all, nor do they only occur in functional programming. In essence, a monad is a design pattern that allows you to chain together operations within a framework. Noticing monadic design can be quite helpful for programmers in any environment, particularly because it’s often undesirable! In many situations, monads have observable tradeoffs, and sometimes (as here) we can even collect concrete data to back this up.
I’m going to try and explain monads in a way that is:
- Geared towards Rust developers, with code samples in Rust, though I hope any sufficiently curious programmer can follow along
- Free of jargon: no mathematical formalism whatsoever
- Without analogies of any kind, and grounded in real programming problems
- Non-trivial: focusing on a production-worthy example with objectively measurable implications
- Practical: with advice all of us coders can use
In other words, I’m going to try and write the monad tutorial that I personally would have appreciated when I was younger. And I’m going to start at a place that’s unconventional: through property-based testing, where monads have profound performance characteristics.
Note: While this article’s primary goal is to explain monads, it also serves as a practical introduction to property-based testing and fault injection techniques. If you’re new to these, you’ll find an introduction to both alongside the monad explanation.
This post consists of five sections:
- Property-based testing goes over the basics
- Drawing the rest of the owl talks about a complex scenario: using property-based testing to inject faults
- Integrated shrinking shows how to reduce inputs of challenging complexity to smaller sizes
- Monads, finally is where we introduce monads in this context, and provide data for how costly they can be
- Rediscovering structure discusses some ways to mitigate the tradeoffs of monads in property-based testing
1. Property-based testing#
Testing is fundamentally about building models for how your code should behave, at just the right level of complexity: they should match the scope of what you’re testing, without going overboard and reinventing the whole system a second time.
The best explication of this general idea I’ve seen is in this piece by the great Argentinian writer Jorge Luis Borges:
…In that Empire, the Art of Cartography attained such Perfection that the map of a single Province occupied the entirety of a City, and the map of the Empire, the entirety of a Province. In time, those Unconscionable Maps no longer satisfied, and the Cartographers Guilds struck a Map of the Empire whose size was that of the Empire, and which coincided point for point with it…”
—On Exactitude in Science, Jorge Luis Borges
Nothing quite exemplifies testing-as-modeling like property-based testing—an approach where instead of specifying exact examples, you define models in terms of properties, or invariants, that your code should satisfy. Then, you test your models against randomly generated inputs.
Let’s take a simple example of a sort function, say my_sort, defined over a slice of integers:
fn my_sort(slice: &mut [u64]) {
// ...
}
How should we go about testing it?
The most common way to do this is to list out a bunch of inputs and ensure they are correctly sorted, through example-based tests.
#[test]
fn test_my_sort() {
let mut input = [1, 2, 0, 2, 0, 5, 6, 9, 0, 3, 1];
my_sort(&mut input);
assert_eq!(input, [0, 0, 0, 1, 1, 2, 2, 3, 5, 6, 9]);
// More examples listed out.
}
Example-based tests are quite valuable, because they are easy to write and quite direct about what happens. But even in a simple example like sorting, it’s easy to imagine cases where your examples don’t quite cover every edge case.
How can more edge cases be covered? Well, one way to do so is to step back and ask, what is the sort trying to do? The goal of a sort function is to ensure that all the elements are in ascending order. Can we test that directly?
The first thing we’d need is to get some inputs to test with. All we care about is a list of numbers here, which seems like it should be easy to generate using a random number generator.
So maybe we write something like:
#[test]
fn test_my_sort_2() {
// Run the test 1024 times.
for _ in 0..1024 {
// Generate a random list of, say, 0 to 512 elements, with values
// between 0 and 10000.
let input = /* ... */;
let mut output = input.clone();
// Call the sort function on it.
my_sort(&mut output);
// Check that all values are in ascending order.
for i in 1..output.len() {
assert!(
output[i - 1] <= output[i],
"input {input:?} failed at index {i}, output {output:?}",
);
}
}
}
We now have a model of sorting that we’ve written down in code form: any pair of values must be in ascending order. (In this view, example-based tests are also simple models: for input X, the output should be Y.)
Now, we run the test, and…
thread 'test_my_sort_2' panicked at tests/tests.rs:33:13:
input [7496, 2087, 6900, 7927, 3840, 3065, 6472, 1186, 6464, 4512, 251, 5591, 3410, 2033, 5367, 2202, 5544, 2434, 6491, 8999, 9818, 2885, 8683, 1201, 6115, 2584, 2473, 6817, 5765, 5196, 9389, 5799, 9012, 293, 38, 1024, 9569, 4654, 7449, 7389, 8088, 5074, 3110, 938, 4944, 3859, 7368, 8978, 7524, 9503, 7406, 7591, 8213, 6445, 7000, 7354, 8967, 5549, 7935, 1866, 4048, 4043, 8905, 3154, 4771, 2364, 3982, 5088, 7317, 233, 3396, 1810, 3022, 9065, 454, 6181, 8257, 9598, 3982, 920, 5880, 4165, 4164, 930, 560, 9062, 5587, 6271, 5878, 2495, 9055, 3877, 4352, 1228, 8287, 8901, 3442, 373, 3635, 5316, 4423, 7688, 7919, 4465, 8991, 7043, 7696, 6875, 1478, 2428, 5127, 6809, 6175, 1415, 7263, 5145, 4153, 876, 1528, 6781, 5627, 6750, 3665, 2567, 6855, 141, 2144, 4491, 9121, 7982, 4131, 6337, 1926, 8797, 9382, 1702, 9559, 3910, 1715, 6661, 269, 4366, 6185, 5616, 365, 808, 4864, 3657, 9574, 3057, 7760, 6375, 2326, 7273, 6303, 7018, 8988, 6271, 988, 7796, 2390, 1689, 4279, 9586, 151, 9738, 3659, 7064, 1529, 8237, 4211, 2272, 8909, 7638] failed at index 173, output [38, 141, 151, 233, 251, 269, 293, 365, 373, 454, 560, 808, 876, 920, 930, 938, 988, 1024, 1186, 1201, 1228, 1415, 1478, 1528, 1529, 1689, 1702, 1715, 1810, 1866, 1926, 2033, 2087, 2144, 2202, 2272, 2326, 2364, 2390, 2428, 2434, 2473, 2495, 2567, 2584, 2885, 3022, 3057, 3065, 3110, 3154, 3396, 3410, 3442, 3635, 3657, 3659, 3665, 3840, 3859, 3877, 3910, 3982, 3982, 4043, 4048, 4131, 4153, 4164, 4165, 4211, 4279, 4352, 4366, 4423, 4465, 4491, 4512, 4654, 4771, 4864, 4944, 5074, 5088, 5127, 5145, 5196, 5316, 5367, 5544, 5549, 5587, 5591, 5616, 5627, 5765, 5799, 5878, 5880, 6115, 6175, 6181, 6185, 6271, 6271, 6303, 6337, 6375, 6445, 6464, 6472, 6491, 6661, 6750, 6781, 6809, 6817, 6855, 6875, 6900, 7000, 7018, 7043, 7064, 7263, 7273, 7317, 7354, 7368, 7389, 7406, 7449, 7496, 7524, 7591, 7638, 7688, 7696, 7760, 7796, 7919, 7927, 7935, 7982, 8088, 8213, 8237, 8257, 8287, 8683, 8797, 8901, 8905, 8909, 8967, 8978, 8988, 8991, 8999, 9012, 9055, 9062, 9065, 9121, 9382, 9389, 9503, 9559, 9569, 9574, 9586, 9598, 9818, 9738]
note: run with `RUST_BACKTRACE=1` environment variable to display a backtrace
Whoops, looks like the function has a bug. (Scroll the above example to the right!)
This example is quite unhelpful and hard to understand! It is possible to use this as an input to debug with, but it is quite painful. If we could use automation to turn this test case into a much smaller one that can still reproduce the bug, debugging becomes significantly easier. The process of doing so is called test case shrinking or reduction.
To recap—property-based testing consists of two components:
- Test case generation using a source of randomness.
- On failing a test, shrinking it down to a smaller, more understandable size.
Implementing a manual shrinker#
What counts as “smaller”? For a list of numbers, ideally we’d be able to minimize both the number of items in the list and the integers themselves. This suggests an algorithm for how to write a shrinker by hand:
First, try and minimize the size of the list using a binary search algorithm. For example:
- Try the first half of the list against the function.
- If that exhibits an error, attempt to recursively shrink this half.
- If that doesn’t work, try it with the last half of the list.
- If neither work or if the list has 1 or fewer elements, move on to the next step.
Once the list has been shrunk, start shrinking the elements within the list, applying binary search to each element.
After you’re done writing this algorithm, you’re well on your way towards creating the original property-based testing library, QuickCheck. This approach has you write two functions: a generator and a shrinker.
With this, you can get much more reasonable-looking output:
input [58, 33] failed at index 1, output [58, 33]
And for relatively simple cases like lists of integers, this kind of shrinking works quite well!
But we’re not here to test simple cases. We’re here for the difficult ones.
2. Drawing the rest of the owl#
Most real-world sort implementations don’t just work over a list of integers. They’re written to be polymorphic over anything which can be sorted. In Rust parlance, this means anything that implements the Ord trait; and even if not, a custom comparator function can be provided.
But Ord can be written by hand, and custom comparators are virtually always written by hand.
One immediate consequence is that it’s possible that the comparator function says two elements are equal, but they are actually different. In that case, should the order of elements be preserved?
- A sort implementation which preserves the order is called a stable sort.
- An implementation which does not is called an unstable sort.
Unstable sorts tend to be faster than stable ones, and there are valid reasons for preferring each at different times. (The Rust standard library has separate implementations for stable and unstable sorts.)
Additionally, hand-written implementations mean users can make mistakes! A production-grade sort algorithm must behave reasonably in the face of arbitrary user input, not just in the actual elements being sorted but also in the comparator function (full credit to Lukas Bergdoll for his extensive research here):
Ord safety: Users can write a comparator that’s simply incorrect. An easy way is to introduce a difference between ordering and equality, for example by returning
Ordering::Lessfor two elements that are actually equal. Users could also return different answers for the same comparison when called at different times1.Panic safety: The comparator can panic in the middle of execution. Since panics can be caught, the input should be in some kind of valid state afterwards.
Observation safety: If any of the inputs are mutated by the comparator, those mutations must be carried through to the final output. (With Rust, mutation through shared references is possible via interior mutability, as seen in
RefCellorMutex).
In these cases, completing the sort successfully becomes impossible. But it’s important that we leave the input in a reasonable state.
How do we go about testing this? Trying to think of all the different failure modes seems really hard! But property-based testing can address this need through randomized fault injection.
Let’s focus on Ord safety for now, with a comparator that flips around the result 20% of the time:
#[derive(Clone, Copy, Debug)]
enum OrdBehavior {
Regular,
Flipped,
}
struct BadType {
value: u64,
ord_behavior: RefCell<Vec<OrdBehavior>>,
}
impl Ord for BadType {
fn cmp(&self, other: &Self) -> Ordering {
// Get the next behavior from the list.
match self.ord_behavior.borrow_mut().pop() {
Some(OrdBehavior::Regular) | None => {
self.value.cmp(&other.value)
}
OrdBehavior::Flipped => {
// Flip the behavior.
other.value.cmp(&self.value)
}
}
}
}
To generate a BadType:
fn generate_bad_type() -> BadType {
// Generate a value between 0 and 10000;
let value = /* ... */;
// Generate a list of behaviors of length 0..128, where the elements are
// Regular 4/5 times and Flipped 1/5 times.
let ord_behavior: Vec<OrdBehavior> = /* ... */;
BadType {
value,
ord_behavior: RefCell::new(ord_behavior),
}
}
And to test this:
#[test]
fn test_my_sort_3() {
// Run the test 1024 times.
for _ in 0..1024 {
// Generate a list of BadTypes using generate_bad_type.
let input: Vec<BadType> = /* ... */;
// Call sort as before.
let mut output = input.clone();
my_sort(&mut output);
// Sorting isn't really well-defined in this case, but we can
// ensure two properties:
//
// 1. my_sort doesn't panic (implicitly checked by getting here)
// 2. all the input values are still present in the output
let mut input_values: Vec<u64> =
input.iter().map(|v| v.value).collect();
let mut output_values: Vec<u64> =
output.iter().map(|v| v.value).collect();
// Sort the input and output values, and assert that they match.
my_sort(&mut input_values);
my_sort(&mut output_values);
assert_eq!(input_values, output_values);
}
}
Our original approach continues to work well—that is, right until the test finds a bug and we need to shrink a failing input.
3. Integrated shrinking#
How does one go about writing a shrinker for Vec<BadType>? Doing so seemed relatively straightforward for a list of integers. But this is a list where the elements are pairs of an integer and another list. Also:
We’ve just tested Ord safety so far—once we’ve added fault injection for other kinds of safety, the complexity seems endless.
And even more importantly, there isn’t a great way to compose smaller shrinkers together to form larger ones. Writing shrinkers is a lot of work already, and what’s the point if you have to keep doing all of it over and over?
The practical result is that most of the time, writing a shrinker for types like Vec<BadType> is quite difficult. And writing one is also technically optional, since:
- If the test passes, shrinkers are never invoked. Simply write correct code, and shrinking just isn’t an issue!
- If the test fails, developers can debug using the original input. It’s painful but possible.
All in all, given the choice of writing a shrinker by hand or just moving on with their lives, most developers tend to choose the latter2. Because of this, most modern property-based testing frameworks, like proptest in Rust, try and take care of shrinking for you through some notion of integrated shrinking.
The idea behind integrated shrinking is: When you generate a random input, you don’t just generate the value itself. You also generate some context that is helpful for reducing the size of the input.
- In proptest, this combined value and context is called a value tree.
- Any implementation that accepts a random number generator and turns it into a value tree is called a strategy.
The proptest library comes with many different kinds of strategies that can be composed together to create more complex ones. To generate an instance of OrdBehavior, we’re going to use two strategies:
- The
Juststrategy, which “just” returns a single value. - The
prop_oneofstrategy, which generates values from one of a possible list of strategies, where each choice has a given probability. (A function that takes one or more strategies as input, and produces a strategy as its output, is called a combinator.)
fn generate_ord_behavior() -> impl Strategy<Value = OrdBehavior> {
prop_oneof![
// 4/5 chance that the Regular implementation is generated.
4 => Just(OrdBehavior::Regular),
// 1/5 chance that it's flipped.
1 => Just(OrdBehavior::Flipped),
]
}
To generate BadType, we’re going to use generate_ord_behavior, as well as:
- A range strategy such as
0..10000_u64, which generates values within the range uniformly at random. - The
veccombinator, which accepts a strategy for elements and a size parameter.
fn generate_bad_type() -> impl Strategy<Value = BadType> {
// Use the range strategy to generate values uniformly at random.
let value_strategy = 0..10000_u64;
// Use the vec strategy to generate a list of behaviors: 0..128 items.
let ord_behavior_strategy = vec(generate_ord_behavior(), 0..128);
// Now what? We need to compose these strategies together. With proptest,
// the way to do this is to first create a tuple of strategies.
let tuple_strategy = (value_strategy, ord_behavior_strategy);
// A tuple of strategies is also a strategy! Generated values are a tuple
// of constituents.
//
// With this in hand, we can use a function called `prop_map` to turn the
// tuple into a BadType.
tuple_strategy.prop_map(|(value, ord_behavior)| {
BadType {
value,
ord_behavior: RefCell::new(ord_behavior),
}
})
}
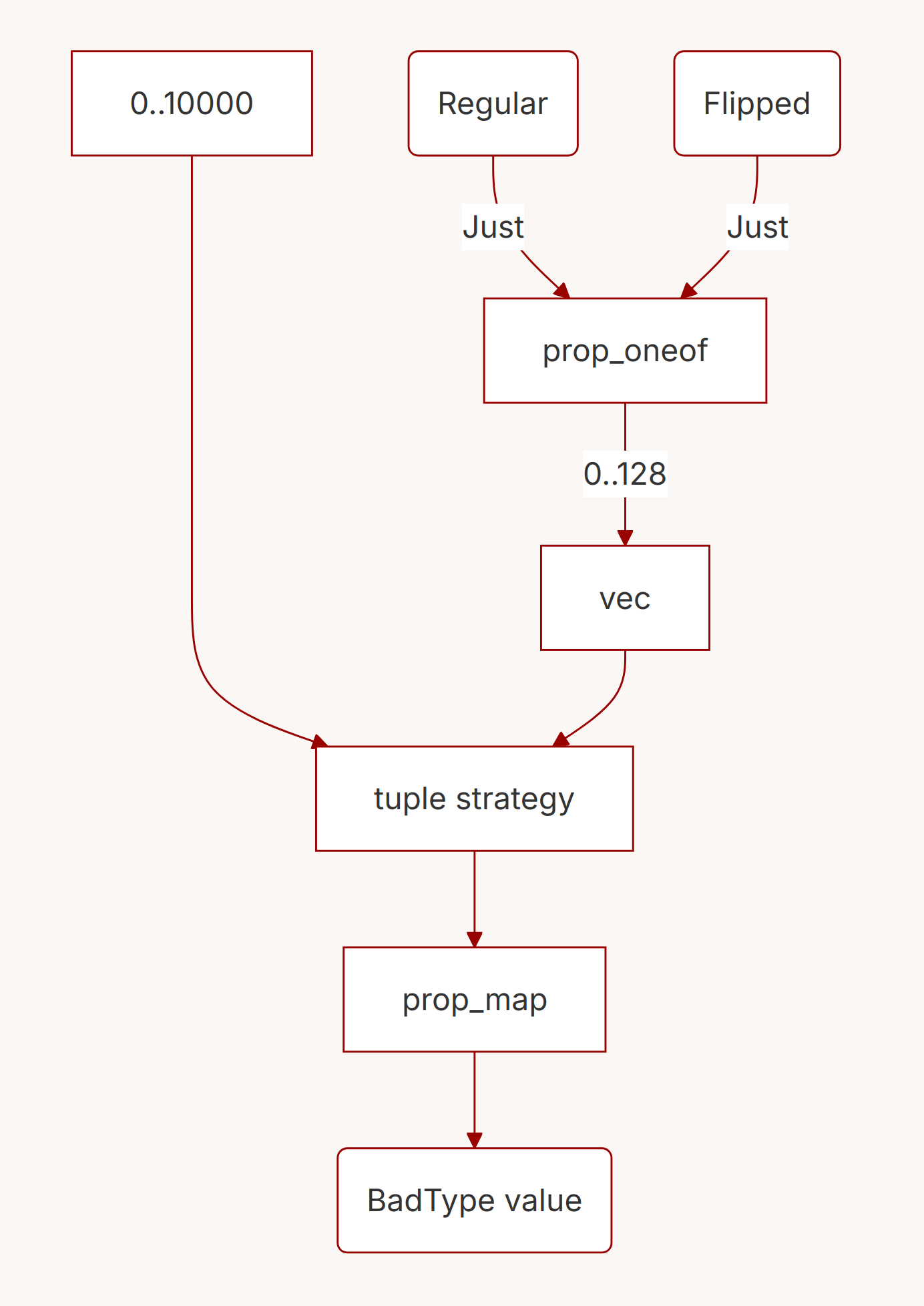
BadType.You might be wondering where all the shrinking code is. It’s actually implemented on the corresponding value trees for each strategy:
- Range strategies use binary search to make values smaller.
- The
Juststrategy doesn’t do any shrinking, since it just returns a single value. - The
prop_oneofcombinator shrinks towards the beginning of the choices: in this case,Flippedis shrunk intoRegular. - The
veccombinator implements roughly the algorithm in Implementing a manual shrinker above.
You can see how the base strategies get turned into successively larger ones through combinators like prop_oneof. It’s very similar to Iterator, where you can keep calling .map, .filter, .enumerate and so on over and over3.
In my experience, composability across different scales is where this model shines. You can build bigger strategies out of smaller ones, up to a surprising amount of complexity. This means that your team can invest in a library of ever-more-complex strategies, and continue to derive value out of that library across everything from the smallest of unit tests to large integration tests.
But there is one massive wrinkle with integrated shrinking. And that wrinkle is exactly what monads are about.
4. Monads, finally#
In the previous few sections, we’ve built up all the context we need. We’re now going to look at the fundamental operation that introduces monadic composition to proptest: prop_flat_map.
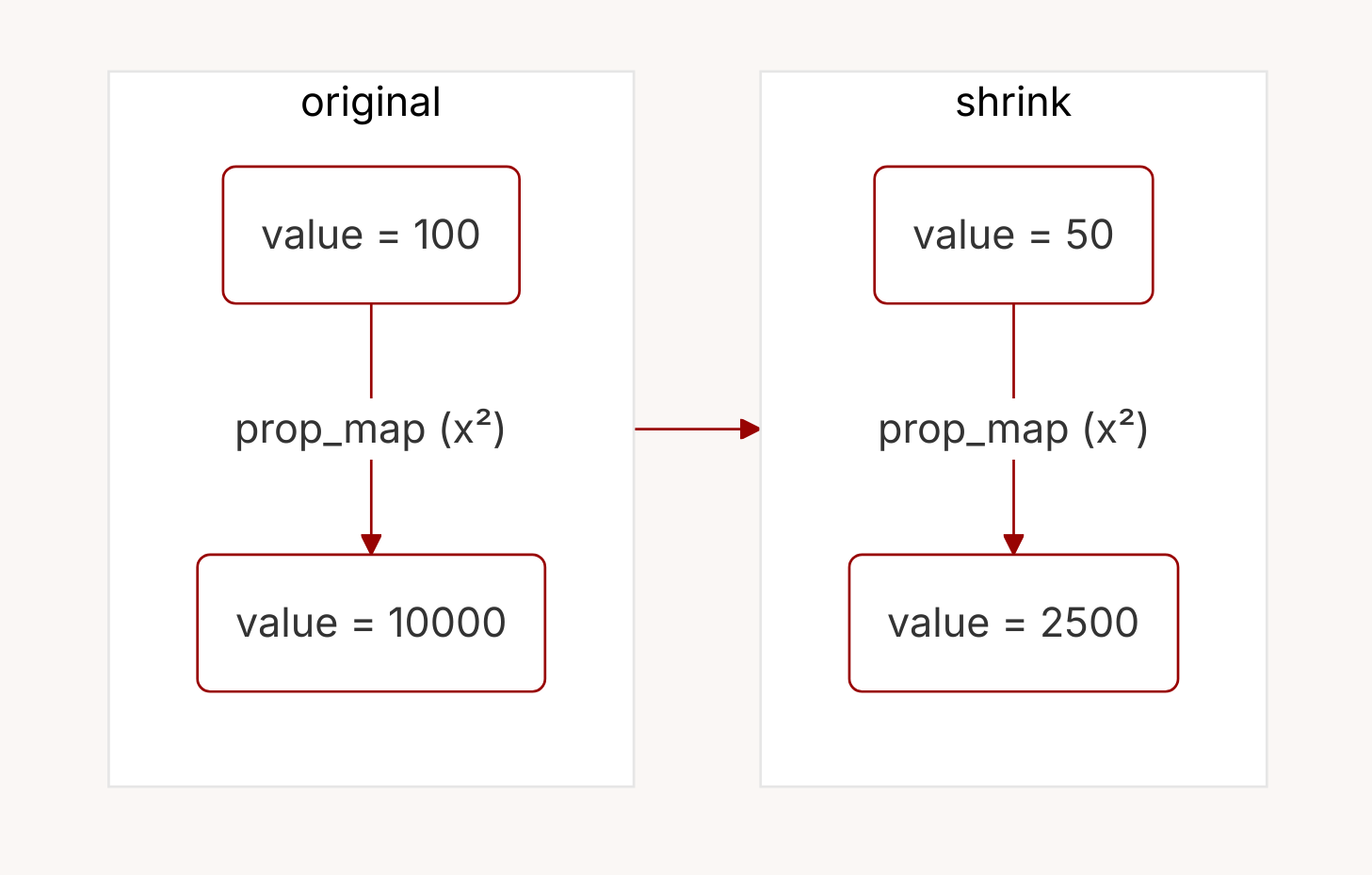
prop_map from x to x². When values are shrunk, they transparently pass through the map function.In the example above, there’s a function called prop_map, which we use to turn a tuple of components into a BadType value. What happens when you try and shrink a value through a prop_map? It’s very simple:
- Attempt to get a smaller value from the underlying value tree.
- Call the map function on the value.
So prop_map is just a conduit that values pass through: it simply maps a value to another value, and does not change the structure of the value tree in any way.
Now let’s say we want to test out pairs of BadType instances, where the way the second BadType is generated depends on the first. This is a situation where we don’t just want to map a value to another value—we need to generate a whole new strategy based on a value.
This is a fundamental shift:
- As above,
prop_maptransforms a value into another, but preserves the original structure. - This new method,
prop_flat_map, goes well beyond that. Based on the value generated, it creates a brand new strategy with a structure all of its own.
This is monadic composition in action. The result of one operation controls, at runtime, the entire shape of the next operation.
For example, here’s one way to go about generating pairs of BadTypes, where the second value is always greater than the first:
fn generate_bad_type_pair() -> impl Strategy<Value = (BadType, BadType)> {
// First generate a BadType.
generate_bad_type().prop_flat_map(
|first_bad_type| {
// Now generate a second BadType with a value greater than the first.
(
(first_bad_type.value + 1)..20000_u64,
vec(generate_ord_behavior(), 0..128),
)
.prop_map(move |(second_value, ord_behavior)| {
// Generate the second value.
let second_bad_type = BadType {
value: second_value,
ord_behavior: RefCell::new(ord_behavior),
};
// Return the pair.
(first_bad_type.clone(), second_bad_type)
})
}
)
}
Your first reaction might be: wow, this seems really powerful. And you would be right! You can write whatever you like in the body of a prop_flat_map:
- You can conditionally return one strategy or another, reimplementing
prop_oneof. - You can first generate a size and then return a vector with those many elements, reimplementing the
veccombinator. - You can call
prop_flat_mapagain, as many times as you like.
In a real and quite rigorous sense, prop_flat_map is maximally powerful. Every combinator we’ve talked about, and in fact most of the proptest library, can be written in terms of prop_flat_map.
So why do all these combinators exist? Why don’t we just use prop_flat_map everywhere?
The function actually works reasonably well in practice. It generates random values with the right shape, and shrinks them correctly on a failing input.
But.
Shrinking is really, really slow.
Exponentially slow.
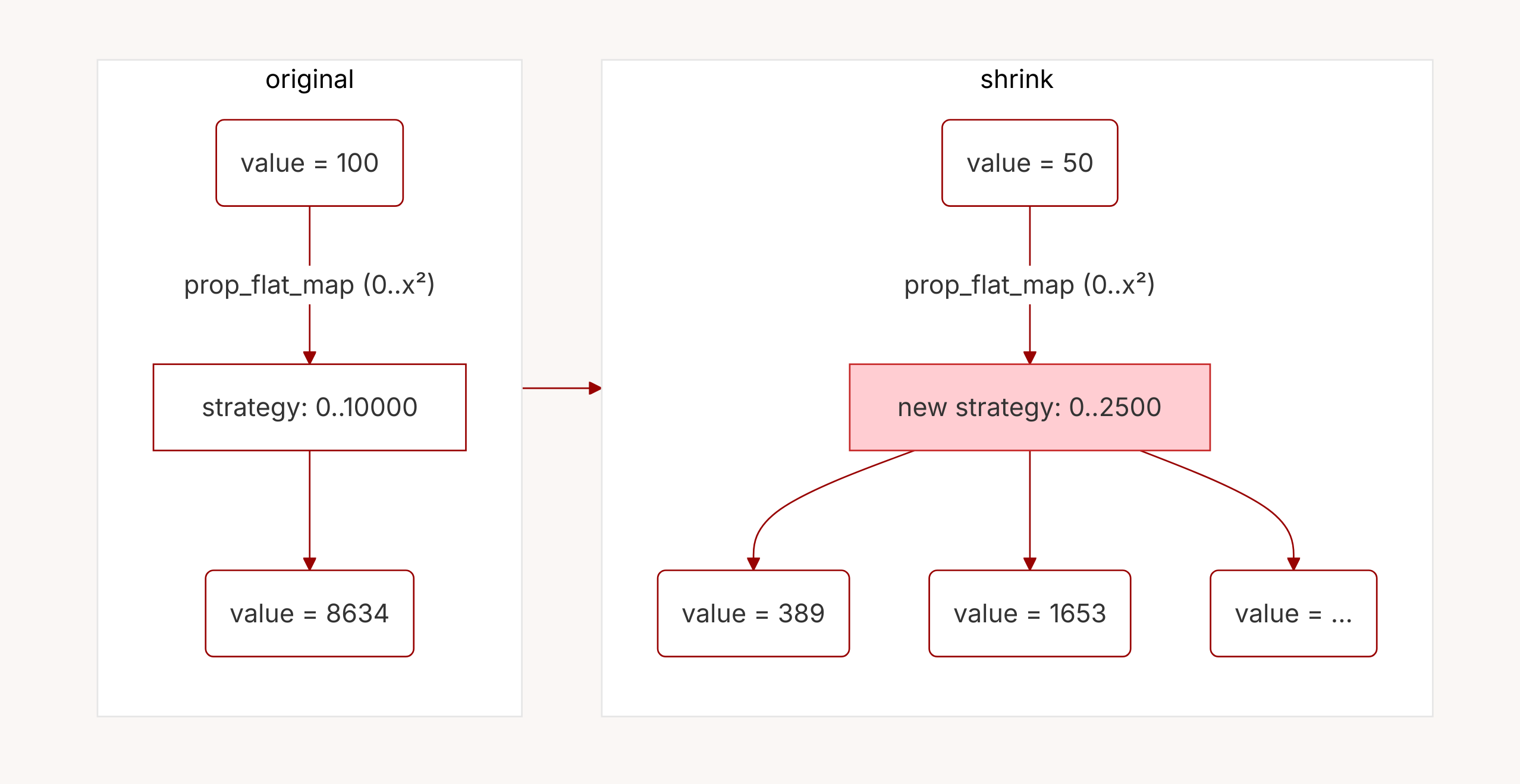
prop_flat_map with a map from x to the strategy 0..x². Each time the original value is shrunk, a brand-new strategy is created (highlighted in red) and the shrinker has to start over.Why is that the case? Consider what happens when we want to shrink a value through a prop_flat_map. As before:
- We would attempt to get a smaller value from the underlying value tree.
- And then, because we would call the
prop_flat_mapcallback to generate a new strategy, we would throw away the previously-generated value tree entirely.
Because prop_flat_map generates brand new value trees each time it’s called, shrinking has to be started again, from scratch, each time! This is the essence of monadic composition: powerful, unconstrained, and fundamentally unpredictable.
Measuring the impact#
We can measure the impact of monadic composition quite directly, along two related axes: the amount of time it takes to complete iterations, and the number of iterations the shrink completes in.
For this post I wrote a small Rust program which collects metrics about shrinking for:
- The
prop_flat_mapimplementations forBadTypepairs above, and a non-monadic implementation withprop_map(see below) - The same for
(BadType, BadType, BadType)triples: a non-monadic implementation withprop_map, and a monadic one with two levels ofprop_flat_map.
With this program, I collected 512 samples on my workstation and analyzed the data. (I ran the program with opt-level set to 1, to mimic typical dev builds in larger Rust projects4).
First, the amount of time it took to shrink values down, by key percentile:
| Metric | Pairs (prop_map) | Triples (prop_map) | Pairs (prop_flat_map) | Triples (prop_flat_map) |
|---|---|---|---|---|
| min | 11 µs | 48 µs | 3.85 ms | 8.95 ms |
| p50 | 1.70 ms | 2.52 ms | 8.52 ms | 181 ms |
| p75 | 3.74 ms | 5.77 ms | 10.04 ms | 307 ms |
| p90 | 5.25 ms | 8.41 ms | 11.76 ms | 435 ms |
| max | 7.00 ms | 10.55 ms | 15.53 ms | 1808 ms |
In this table, p50 represents the median completion time, while p75 and p90 show the times that 75% and 90% of the samples completed within. With prop_map, the amount of time scales somewhat linearly as we go from pairs to triples. But with just one additional level of prop_flat_map, the performance degrades dramatically, going from under 20 milliseconds to almost 2 seconds! That’s over 100x slower.
The difference in the number of iterations is even more striking:
| Metric | Pairs (prop_map) | Triples (prop_map) | Pairs (prop_flat_map) | Triples (prop_flat_map) |
|---|---|---|---|---|
| min | 48 | 93 | 1228 | 11223 |
| p50 | 215 | 306 | 6722 | 281016 |
| p75 | 270 | 354 | 9315 | 481996 |
| p90 | 310 | 410 | 10722 | 693358 |
| max | 387 | 530 | 12242 | 884729 |
From hundreds of iterations to almost a million! And we’re working with pretty simple structures here, too. Just one more level of prop_flat_map would make shrinking quite noticeably slow, and another one after that would be disastrous.
The data here spans several orders of magnitude. A good way to visualize this kind of data is via a CDF plotted on a logarithmic scale. In these graphs, the x-axis shows the time or iterations, and the y-axis shows the cumulative probability. Curves that are further to the right are worse, and the logarithmic scale reveals that the differences are in orders of magnitude.
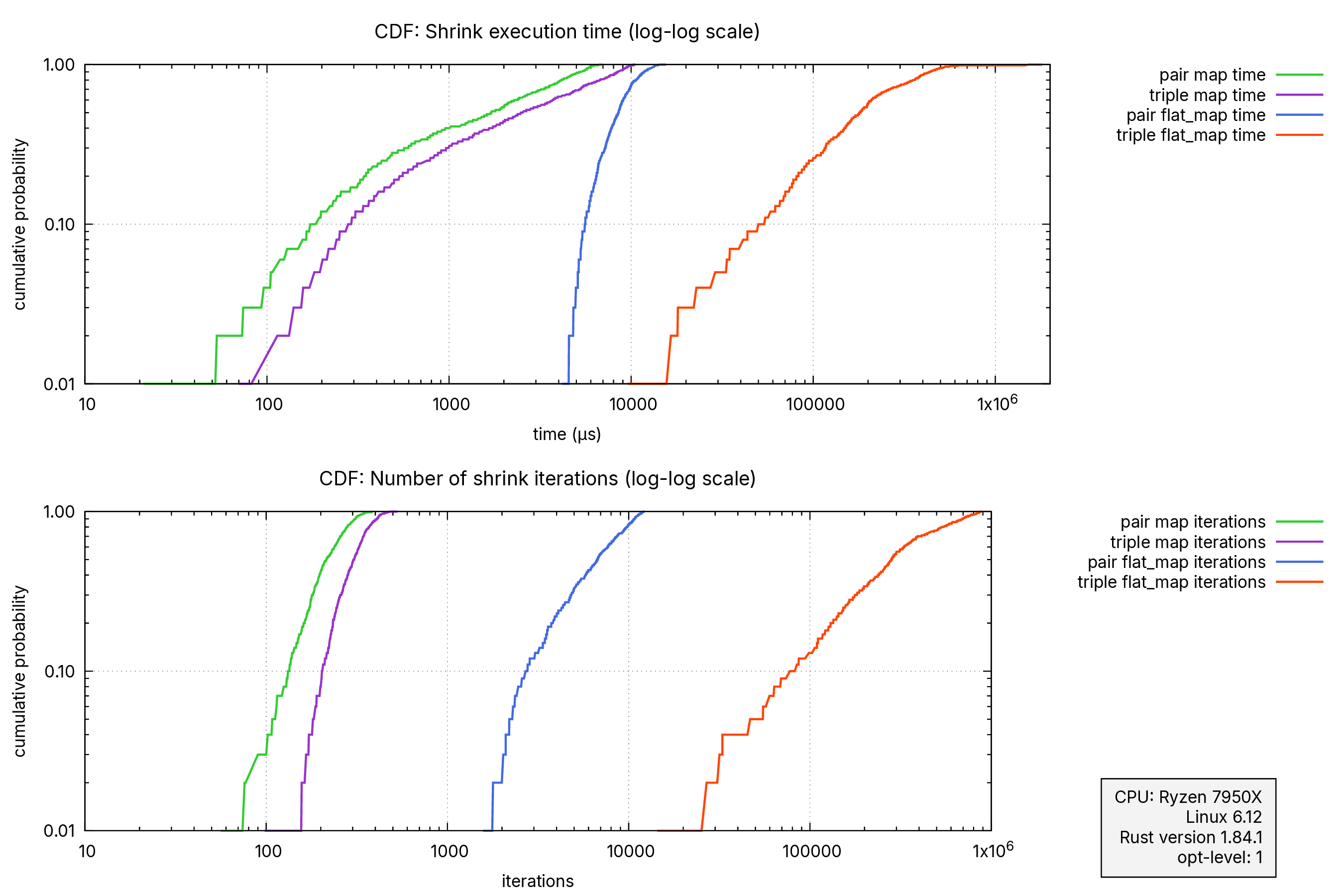
prop_map and prop_flat_map pairs and triples. This is a logarithmic scale, so the differences are in orders of magnitude.5. Rediscovering structure#
What makes monadic composition so difficult to deal with? It has to do with the fact, mentioned above, that you can write whatever you like inside the prop_flat_map. Because a prop_flat_map can contain arbitrary computation inside of it, and that computation returns brand-new strategies, determining how a value will shrink through it is fundamentally unpredictable without actually executing it.
In other words, the prop_flat_map callback is quite opaque. Why is that? It’s because the prop_flat_map callback is written in Rust, which is a powerful, Turing-complete language. It is impossible to fully analyze the semantics of Turing-complete languages5. (You might know this as the halting problem, or as Rice’s theorem.)
But the fact that some analysis requires solving the halting problem is merely the start of the discussion, not the end of it! There is a rich literature on how to find approximate solutions for problems that are otherwise insoluble due to Rice’s theorem. For shrinking, here are a few approaches that are known to work.
One option is to place limits on how long shrinking is done for. Note that prop_flat_map has no issues while generating values, just while shrinking them6. The proptest library itself sets limits on shrink iterations, particularly across prop_flat_map instances. This ensures that shrinking operations finish in a reasonable amount of time, even if they don’t produce minimal values.
A better option is to rewrite generators to not use monadic composition. For the example above, it’s not hugely difficult7:
fn better_generate_bad_type_pair() -> impl Strategy<Value = (BadType, BadType)> {
// Generate two BadType instances.
(
generate_bad_type(),
generate_bad_type(),
)
// Look, no prop_flat_map! This is non-monadic composition.
.prop_map(|(bad1, mut bad2)| {
// Add bad1.value to bad2.value. Because the two are non-negative
// (unsigned integers), this ensures that bad2.value is always
// bigger than bad1.value.
bad2.value += bad1.value;
(bad1, bad2)
})
}
But this can be quite challenging as complexity goes up! The proptest library comes with a number of helpers to write non-monadic strategies, particularly prop_recursive and sample::Index. But there are real situations, particularly with large and complex data structures (for example, randomly-generated programming language syntax trees), where none of those options suffice and you have to use the full power of prop_flat_map.
Last but not least, there’s a set of approaches that I’m going to put into the bucket of rediscovering structure across flat maps. Key to these is understanding that when you generate a random value, you’re turning an RNG, which is a random stream of bits, into concrete, structured values. Can we somehow be clever about looking at the RNG bitstream?
One option is to instrument the test, for example by using a fuzzer. Fuzzing is all about generating random data, looking at the branches explored, and tweaking the random data to ensure other branches are taken. It’s a great fit for peering past the black box of monadic composition.
Another option is to be clever with random number generator. A random number ultimately generates a sequence of ones and zeroes. Can we poke at this sequence, possibly with the help of some hints from the strategies themselves? This is implemented by the Hypothesis framework for Python; see this excellent paper about it.
Both of these approaches are heuristic and quite complex. But that’s what you need to put together some structure again, after it’s been through the blender of monadic composition.
Conclusion: constraints liberate, liberties constrain#

In this article, we looked at monads as a design pattern: a way for a user to compose operations within a framework. We looked at both monadic functions like prop_flat_map, and non-monadic ones such as prop_map and prop_oneof. Finally, we saw how in the context of property-based testing, monadic composition has a performance impact measured in orders of magnitude.
With this knowledge in mind, you can now spot monadic composition in all kinds of other places:
Futures in Rust, where
.awaitis monadic, but futures are awaited sequentially. To run futures concurrently, you have to use non-monadic operations likefuture::join.Some build systems, where individual build nodes can generate more nodes, making it impossible to generate a dependency graph without running the build. (Cargo is thankfully non-monadic.)
And even with iterators, where
Iterator::mapreturns an iterator with the same length as before, andfilter_mapreturns an iterator with the same or a smaller length, but the length offlat_mapis unbounded.Option::and_then,Result::and_then, andResult::or_elseall happen to be monadic operations as well, though they’re all simple enough that they don’t have any practical downsides.
The common thread through all of these examples is that within a framework, monadic composition is not just from value to value. It is from value to a further instance of that framework. The return value of future.await can result in more futures being spawned, monadic build nodes can generate more build nodes, and flat_map turns individual values into iterators. This freedom is what makes monads both the most flexible kind of composition, and the hardest to predict the behavior of.
This is part of a general observation throughout programming, whenever there’s an interaction between two parties or two sides. The more restrictions there are on one side, the freer the other side is to do what it likes. Monadic composition is an extreme version of that: the most powerful and least constrained form of composition for the user, but the most difficult to deal with for the framework.
Whether you’re a user or a library designer, pay close attention to situations where your operations are monadic. They can provide a great deal of power, perhaps too much in some circumstances. If non-monadic operations are sufficient to help you achieve your goal, prefer them.
And when they aren’t enough: well, now you know what you’re getting into!
Thanks to Fiona and Cliff Biffle for reviewing drafts of this post. Any mistakes in it are my own.
Updated 2025-02-20: Clarified note about Turing completeness to indicate that it is not the composition itself that’s Turing-complete—it’s the language used to write the callback in that’s at issue.
Appendix#
This section contains some jargon, but it’s mostly here to satisfy the pedants who will inevitably Ctrl-F for “monad laws”. Please ignore this section if you didn’t get here through a search for that string.
Click to expand
Formally speaking, monads are any kind of structure with two operations return and bind, where these operations obey three monad laws. For Strategy, these functions would be:
fn return<T>(x: T) -> impl Strategy<Value = T>;
fn bind<U, ST, F, SU>(base: ST, f: F) -> impl Strategy<Value = U>
where
ST: Strategy,
F: Fn(ST::Value) -> SU,
SU: Strategy<Value = U>;
For strategies, return is Just, and bind is prop_flat_map.
Here are the three monad laws expressed in terms of proptest:
Left identity: for any
value,Just(value).prop_flat_map(f)should be the same asf(value). That is indeed the case, both for generation and for shrinking. SinceJustdoes not do any shrinking, the pathologicalprop_flat_mapbehavior doesn’t take effect.Right identity: for any
strategy,strategy.prop_flat_map(Just)should be the same asstrategy. That is also the case. Every timestrategyis shrunk,prop_flat_maphas to discard the state returned by the dependent strategy. ButJustis a trivial strategy that doesn’t have any state, so it’s effectively a no-op.Associativity: if you have a chain of two
prop_flat_maps, you can apply the second one either “inside” or “outside” the first one. More specifically, for anystrategy, with the definitions:let strat1 = strategy.prop_flat_map(f).prop_flat_map(g); let strat2 = strategy.prop_flat_map(|value| f(value).prop_flat_map(g));this law requires that
strat1andstrat2are the same. That’s true as well, both for generation and for shrinking, though the latter is slightly harder to see.
One might object by pointing out that in Rust, the above operations result in different types even if they have the same behavior. That is true, but also not particularly relevant, since you can always call Strategy::boxed to erase the type.
One might also point out that we haven’t talked about a Monad typeclass or trait here. That’s a distraction! Monadic composition exists everywhere in programming, regardless of whether the language lets you express Monad as a reified type. You can express Monad in modern versions of Rust via GATs, but there really isn’t much utility to it.
Thank you!
Some of these examples might seem far too adversarial to ever be seen in the real world. But an implementation that can handle adversarially bad inputs can also handle inputs that are bad in more benign ways. For production-grade sort functions, it makes sense to design for the worst possible inputs. ↩︎
This is not a moral failing on the part of those developers, because free will doesn’t exist. It’s completely fine, and worth embracing! Integrated shrinking is altering the environment in action. ↩︎
Just like with iterators, the type signatures also become quite long! ↩︎
The default value of
opt-level, 0, is fine forprop_map, but infeasible forprop_flat_mapwith triples. ↩︎The problem is not specific to Turing-complete languages—it even exists in non-Turing-complete ones. For example, if the callback were written in a language that only had for loops, no while loops, the framework would still not be able to peer past the shrinker. ↩︎
I think this is the key insight that many monad tutorials miss. When writing about monads, it’s tempting to focus on simple examples like
Option::and_then, where the monadic behavior doesn’t have significant practical implications. Here, too, if we restrict ourselves to generating values, there’s nothing wrong withprop_flat_map. It’s only during shrinking that monadic composition rears its ugly head.If you’re explaining monads to an audience, consider emphasizing not just what monads are, but when their unconstrained power becomes a liability rather than an asset. ↩︎
If you’re playing close attention, you might notice that while this function meets the requirement we set out, the random distribution generated is somewhat different. In this case, it’s possible to get a distribution equivalent to the
prop_flat_mapexample through the use ofsample::Index. ↩︎